Modeling the equilibrium shape of adsorbed vesicles of lipid bilayers

Translations: FR

Lipid bilayers are often taken as experimental models for biological membranes. In many cases, the investigation of their biochemical properties, such as their chemical affinity for one or the other conpound, is carried out either on adsorbed vesicles or on bilayers supported by solid subtrates. For these studies, neutron reflectivity is an exceptional tool (see for instance the impresive list of experiments in this field that have been done on MARIA neutron reflectometer ). However, with neutron reflectivity the data analysis (in jargon “data fitting”) is really a tricky problem. Reducing the number of free parameters is crucial. In the case of adsorbed vesicles this can be done by modeling the equilibrium shape that they adopt depending on some physical parameters (rigidity, adsorption constant, size etc.).

To be rigorous, this modeling (finding which surface shape minimizes the free energy of vesicles) should involve variational calculus with Lagrange multipliers leading to a third- or fourth-order nonlinear partial differential equation. This cumbersome and time consuming method is inapropriate for the fitting of reflectivity data which itself is already time consuming. I have developped a light method (implemented as a Python library) allowing the problem to be reduced in one dimension (finding which line of revolution minimizes the free energy).

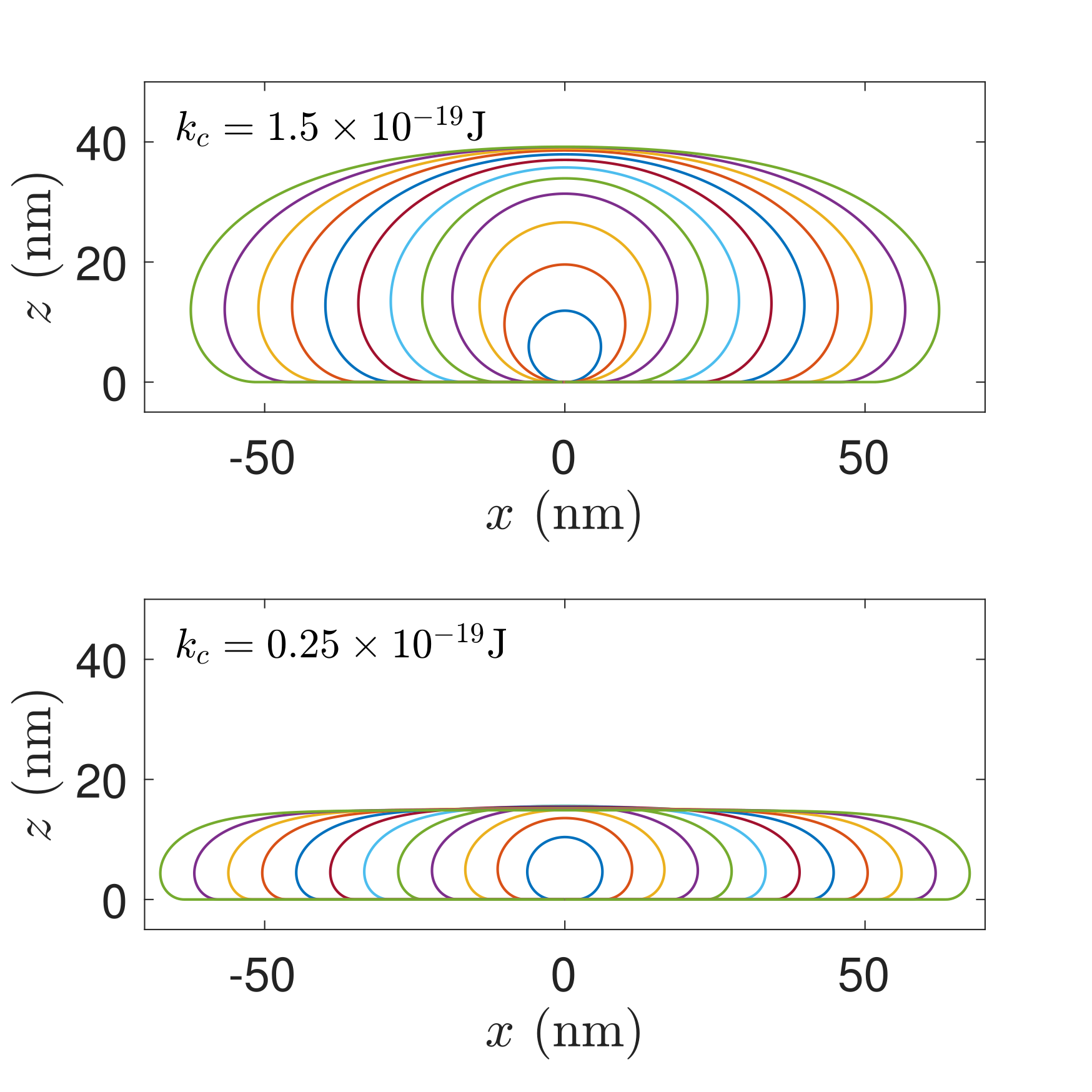
/fig_shape.png
Equilibrium shapes of adsorbed vesicles of different sizes (colors) for two values of the rigidity (kc) and a given adsorption constant.

The method has been applied to concrete exemples.